3の倍数になる条件は？

3の倍数になる数字は？

3の倍数であれば、各桁の数字を足し合わせると和が3の倍数になる（例：357→3+5+7＝15は3の倍数）。
キャッシュ

さんの倍数判定は？

なんということでしょう…。実は各桁の数を足すだけで、3の倍数かどうかがわかるのです！実際に「1122」の各桁を足すと「1+1+2+2=6」となり、3の倍数です。このことから「1122」も3の倍数であることがわかります！
キャッシュ

4の倍数になる条件は？

4の倍数は、下2ケタが4で割り切れたら4の倍数で、そうでないなら4の倍数ではないんだ。例えば、9924は、下2ケタの「24」が4で割り切れるので、4の倍数だね。 1111は、下2ケタの「11」が4で割り切れないので、4の倍数ではない。

5の倍数になる数は何ですか？

5の倍数は、下1ケタが0，5なら5の倍数で、そうでないなら5の倍数ではない。余裕があれば、このポイントが成り立つ理由もおさえておこう。ある整数について、一の位の数をのぞいた部分は、9990、86430などのように、必ず10の倍数になるよね。

7の倍数かどうか？

一の位が偶数で、各ケタの和が3の倍数である。・一の位から3ケタごとに区切り、それらを交互に加減した結果が7の倍数である。・（１の位を消した数）+（消した１の位の数を 5 倍した数）が7の倍数である。

3の倍数の素数はいくつですか？

解法１ nを3k,3k+1,3k+2に場合分けして、３の倍数であることを証明します。３の倍数の素数は「３」のみである。

3と4の公倍数は何の倍数になっていますか？

2つ以上の整数に共通な倍数。 3と4の公倍数は12、24、36、… 最小公倍数…公倍数の中で最小の整数。 ※公倍数は最小公倍数の倍数になる。

3の倍数の特徴は？

まとめ 3の倍数の見つけ方は、「各位の数字の和が 3で割り切れれば、その数字は 3の倍数である。」

2の倍数の条件は？

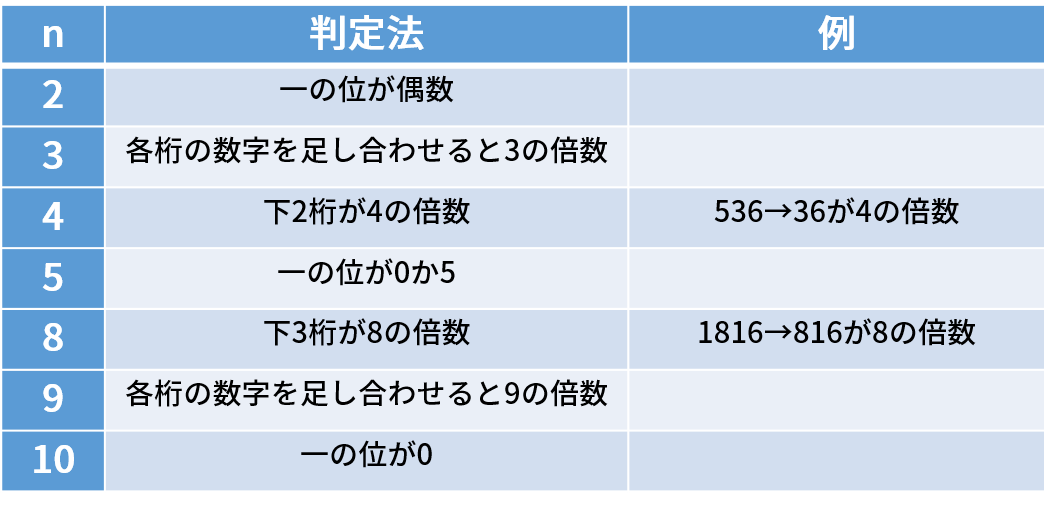
よく使われる倍数判定法

・2,4,5の倍数判定先ほどの例でも扱ったように、2の倍数かどうかは1の位の数に注目し、それが2で割り切れる数（0,2,4,6,8のどれか）であれば2の倍数、そうでなければ2の倍数ではない、つまり奇数だとわかります。

12の倍数は何ですか？

12 の倍数 ⇒ 12，24，36，48，60，72 …

3と7の公倍数は何ですか？

３と７の公倍数は、３と７の最小公倍数２１の倍数になっています。３の倍数と７の倍数の共通している部分が３と７の公倍数だね。２４は１，２，３，４，６，８，１２，２４でわりきれます。この１，２，３，４，６，８，１２，２４を２４の約数といいます。

13は何で割れる？

1	1より大きくない
12	2,3,4,6で割り切れる
13	素数
14	2,7で割り切れる
15	3,5で割り切れる

素数 3 なぜ？

素数とは、約数を2つしかもたない数のこと。ある数の約数がとの2つしかないとき（逆に言うと、答えがとなる自然数の掛け算は 1 × n しかないとき）、その数を素数という。は 1 × 2 でしか作ることができないので素数、も 1 × 3 でしか作ることができないので素数。

3と7の公倍数はいくつですか？

3の公倍数とは何ですか？

いくつかの整数の共通な倍数を公倍数というよ。倍数は，ある整数を1倍，2倍，3倍…にした数のことだね。例えば，2と3の公倍数は，2の倍数にも3の倍数にもなっている数のことだよ。

3で割れる法則は？

知っているととても便利なので、この機会にぜひ覚えておきましょう。各ケタの数字の和（足し算の答え）が3の倍数ならば、その数は3の倍数です。 3の倍数、すなわち3で割り切れるという意味です。

8の倍数になる条件は？

簡単!! 8の倍数の見分け方下(しも)三桁を2で割る。( 割れなければ 8の倍数ではない)2で割った答え(商)の下(しも)二桁が4の倍数であれば、元の数字は8の倍数。

48はなんの倍数？

48＝6×8だから、48は8番目の6の倍数。

3と4の倍数は何ですか？

3と4の公倍数は12、24、36、… 最小公倍数…公倍数の中で最小の整数。

4と7の倍数は何ですか？

（例） 4の倍数 4 , 8 , 12 , 16 , 20 , 24 , 28 , 32 , 36 , 40 , 44 , 48 , 52 , 56 , 60 , … 7の倍数 7 , 14 , 21 , 28 , 35 , 42 , 49 , 56 , 63 , 70 , 77 , 84 , 91 , 98 , …

News